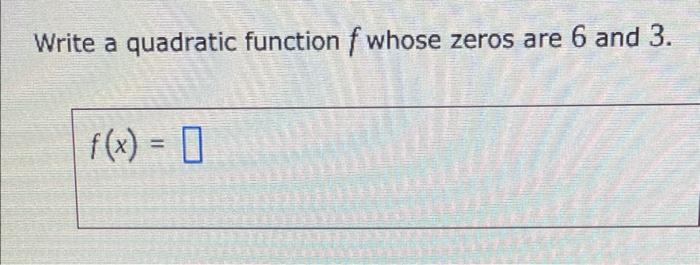
Write a quadratic function whose zeros are and – Embark on an enlightening journey into the realm of quadratic functions, where we unravel the intricacies of defining and constructing these functions with prescribed zeros. Delve into the fundamental concepts that govern their behavior and explore their captivating applications in the real world.
Quadratic functions, characterized by their parabolic shape, are ubiquitous in various scientific and engineering disciplines. Understanding how to construct these functions with specific zeros is paramount for modeling a diverse range of phenomena, from projectile motion to optimization problems.
Quadratic Functions and Their Zeroes: Write A Quadratic Function Whose Zeros Are And

Quadratic functions are mathematical expressions that describe a parabola. They are widely used in various fields, including physics, engineering, and economics. Understanding their properties and how to work with them is essential for solving problems involving parabolic trajectories, optimization, and more.
1. Defining a Quadratic Function
A quadratic function is a polynomial function of degree 2. Its standard form is y = ax² + bx + c, where a, b, and c are constants and a ≠ 0. The graph of a quadratic function is a parabola, which opens upward if a > 0 and downward if a< 0.
The coefficients a, b, and c play crucial roles in determining the shape and behavior of the parabola. The coefficient a affects the width of the parabola, with larger values resulting in a narrower parabola. The coefficient b affects the vertical shift of the parabola, and the coefficient c represents the y-intercept.
2. Zeroes of a Quadratic Function, Write a quadratic function whose zeros are and
The zeroes of a quadratic function are the x-coordinates of the points where the parabola intersects the x-axis. They represent the values of x for which y = 0. The zeroes can be found using the quadratic formula: x = (-b ± √(b² – 4ac)) / 2a.
The discriminant, b² – 4ac, determines the number and nature of the zeroes. If b² – 4ac > 0, the quadratic function has two distinct real zeroes. If b² – 4ac = 0, the function has one real double zero.
If b² – 4ac< 0, the function has no real zeroes and instead has two complex conjugate zeroes.
3. Quadratic Function with Given Zeroes
Given two zeroes, p and q, the quadratic function can be written in the factored form: y = a(x – p)(x – q). The coefficient a can be determined by substituting one of the zeroes into the function and solving for a.
For example, if the zeroes are p = 2 and q = -3, the quadratic function can be written as y = a(x – 2)(x + 3). Substituting p = 2, we get y = a(2 – 2)(2 + 3) = 10a.
Therefore, a = 1 and the quadratic function is y = (x – 2)(x + 3).
4. Examples and Applications
Quadratic functions have numerous applications in various fields. Here are a few examples:
- Projectile Motion:The trajectory of a projectile thrown into the air can be modeled using a quadratic function, with the height of the projectile as a function of time.
- Optimization:Quadratic functions are used to find the maximum or minimum values of a function. This is useful in optimization problems, such as finding the minimum cost or maximum profit.
- Circuit Analysis:Quadratic functions are used to analyze the behavior of electrical circuits, particularly in the study of resonance and filter design.
User Queries
What is the standard form of a quadratic function?
The standard form of a quadratic function is y = ax² + bx + c, where a, b, and c are real numbers and a ≠ 0.
How do I find the zeros of a quadratic function?
The zeros of a quadratic function can be found using the quadratic formula: x = (-b ± √(b² – 4ac)) / 2a.
How do I construct a quadratic function with prescribed zeros?
To construct a quadratic function with prescribed zeros, p and q, use the formula: y = a(x – p)(x – q), where a is a non-zero constant.